Introducing tidygraph
I’m very pleased to announce that my new package tidygraph is now available on CRAN. As the name suggests, tidygraph is an entry into the tidyverse that provides a tidy framework for all things relational (networks/graphs, trees, etc.). tidygraph is a relatively big package in terms of exported functions (280 exported symbols) so all functions will not be covered in this release note. I will however provide an overview of all the areas that tidygraphtouches upon so you should have a pretty good grasp on what the package can do for you.
Tidy network data?
There’s a discrepancy between relational data and the tidy data idea, in that relational data cannot in any meaningful way be encoded as a single tidy data frame. On the other hand, both node and edge data by itself fits very well within the tidy concept as each node and edge is, in a sense, a single observation. Thus, a close approximation of tidyness for relational data is two tidy data frames, one describing the node data and one describing the edge data.
The tbl_graph object
Underneath the hood of tidygraph lies the well-oiled machinery of igraph, ensuring efficient graph manipulation. Rather than keeping the node and edge data in a list and creating igraph objects on the fly when needed, tidygraph subclasses igraph with the tbl_graph class and simply exposes it in a tidy manner. This ensures that all your beloved algorithms that expects igraph objects still works with tbl_graph objects. Further, tidygraph is very careful not to override any of igraphs exports so the two packages can coexist quite happily.
To underline the tidyness of the tbl_graph class the print method shows the object as two tibbles along with additional network information.
library(tidygraph)
create_ring(10)
#> # A tbl_graph: 10 nodes and 10 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 10 x 0 (active)
#> #
#> # Edge Data: 10 x 2
#> from to
#> <int> <int>
#> 1 1 2
#> 2 2 3
#> 3 3 4
#> # ... with 7 more rows
tbl_graph objects can be created directly using the tbl_graph() function that takes a node data.frame and an edge data.frame. On top of that, tidygraph also provides coercion from a huge amount of relational data structures. The following list gives the packages/classes that can currently be converted to tbl_graphs, using the as_tbl_graph function:
-
data.frame,list,matrixfrombase -
igraphfromigraph -
networkfromnetwork -
dendrogramandhclustfromstats -
Nodefromdata.tree -
phyloandevonetfromape -
graphNEL,graphAM,graphBAMfromgraph(in Bioconductor)
For all of the coercions you can expect that data on the nodes and edges are kept and available after conversion to tbl_graph:
iris_clust <- hclust(dist(iris[1:4]))
iris_tree <- as_tbl_graph(iris_clust)
iris_tree
#> # A tbl_graph: 299 nodes and 298 edges
#> #
#> # A rooted tree
#> #
#> # Node Data: 299 x 4 (active)
#> height leaf label members
#> <dbl> <lgl> <fctr> <int>
#> 1 0.0000000 TRUE 108 1
#> 2 0.0000000 TRUE 131 1
#> 3 0.2645751 FALSE 2
#> 4 0.0000000 TRUE 103 1
#> 5 0.0000000 TRUE 126 1
#> 6 0.0000000 TRUE 130 1
#> # ... with 293 more rows
#> #
#> # Edge Data: 298 x 2
#> from to
#> <int> <int>
#> 1 3 1
#> 2 3 2
#> 3 7 5
#> # ... with 295 more rows
Lastly, tidygraph also wraps the multitude of graph constructors available in igraph and exports them under the create_() family of functions for deterministic constructors (e.g. the call to create_ring(10) above) and the play_() family for constructors that incorporate sampling (e.g. play_erdos_renyi() for creating graphs with a fixed edge probability). All of these functions provide a consistent argument naming scheme to make them easier to use and understand.
Meet a new verb…
There are many ways a multitable setup could fit into the tidyverse. There could be an added qualifier to the verbs such as mutate_nodes() and filter_edges() or each verb could take an additional argument specifying what is targeted e.g. arrange(…, target = ‘nodes’). Both of these approachable are viable but would require a huge amount of typing as well as being taxing to support down the line.
The approach used by tidygraph is to let the data object itself carry around a pointer to the active data frame that should be the target of manipulation. This pointer is changed using the activate() verb, which, on top of changing which part of the data is being worked on, also changes the print output to show the currently active data on top:
iris_tree %>% activate(edges)
#> # A tbl_graph: 299 nodes and 298 edges
#> #
#> # A rooted tree
#> #
#> # Edge Data: 298 x 2 (active)
#> from to
#> <int> <int>
#> 1 3 1
#> 2 3 2
#> 3 7 5
#> 4 7 6
#> 5 8 4
#> 6 8 7
#> # ... with 292 more rows
#> #
#> # Node Data: 299 x 4
#> height leaf label members
#> <dbl> <lgl> <fctr> <int>
#> 1 0.0000000 TRUE 108 1
#> 2 0.0000000 TRUE 131 1
#> 3 0.2645751 FALSE 2
#> # ... with 296 more rows
As can be seen, activate() takes a single argument specifying the part of the data that should be targeted for subsequent operations as an unquoted symbol. tidygraph continues the naming conventions from ggraph using nodes and edges to denote the entities and their connections respectively, but vertices and links are allowed synonyms inside activate().
The current active data can always be extracted as a tibble using as_tibble()
as_tibble(iris_tree)
#> # A tibble: 299 x 4
#> height leaf label members
#> <dbl> <lgl> <fctr> <int>
#> 1 0.0000000 TRUE 108 1
#> 2 0.0000000 TRUE 131 1
#> 3 0.2645751 FALSE 2
#> 4 0.0000000 TRUE 103 1
#> 5 0.0000000 TRUE 126 1
#> 6 0.0000000 TRUE 130 1
#> 7 0.3464102 FALSE 2
#> 8 0.5196152 FALSE 3
#> 9 0.5567764 FALSE 5
#> 10 0.0000000 TRUE 119 1
#> # ... with 289 more rowsThe dplyr verbs
Using activate() it is possible to use the well known dplyr verbs as one would expect without much hassle:
iris_tree <- iris_tree %>%
activate(nodes) %>%
mutate(Species = ifelse(leaf, as.character(iris$Species)[label], NA)) %>%
activate(edges) %>%
mutate(to_setose = .N()$Species[to] == 'setosa')
iris_tree
#> # A tbl_graph: 299 nodes and 298 edges
#> #
#> # A rooted tree
#> #
#> # Edge Data: 298 x 3 (active)
#> from to to_setose
#> <int> <int> <lgl>
#> 1 3 1 TRUE
#> 2 3 2 TRUE
#> 3 7 5 TRUE
#> 4 7 6 TRUE
#> 5 8 4 TRUE
#> 6 8 7 NA
#> # ... with 292 more rows
#> #
#> # Node Data: 299 x 5
#> height leaf label members Species
#> <dbl> <lgl> <fctr> <int> <chr>
#> 1 0.0000000 TRUE 108 1 setosa
#> 2 0.0000000 TRUE 131 1 setosa
#> 3 0.2645751 FALSE 2 <NA>
#> # ... with 296 more rows
In the above the .N() function is used to gain access to the node data while manipulating the edge data. Similarly .E() will give you the edge data and .G() will give you the tbl_graph object itself.
Some verbs have effects outside of the currently active data. filter()/slice() on node data will remove the edges terminating at the removed nodes and arrange() on nodes will change the indexes of the to and from column in the edge data.
While one might expect all of dplyrs verbs to be supported in that manner, there is a clear limitation in the relational data structure that requires rows to maintain their identity. Thus, summarise() and do() are not allowed as there is no clear interpretation of how alterations on the node and edge data with these verbs should be interpreted. If these operations are required I suggest applying them to a tibble representation and then joining the result back in.
Speaking of joining, all joins from dplyr are supported. Nodes and edges are added and removed as required by the join. New edge data to be joined in must have a to and from column referencing valid nodes in the existing graph.
library(dplyr)
iris_sum <- iris %>%
group_by(Species) %>%
summarise_all(mean) %>%
ungroup()
iris_tree <- iris_tree %>%
activate(nodes) %>%
left_join(iris_sum)
iris_tree
#> # A tbl_graph: 299 nodes and 298 edges
#> #
#> # A rooted tree
#> #
#> # Node Data: 299 x 9 (active)
#> height leaf label members Species Sepal.Length Sepal.Width
#> <dbl> <lgl> <fctr> <int> <chr> <dbl> <dbl>
#> 1 0.0000000 TRUE 108 1 setosa 5.006 3.428
#> 2 0.0000000 TRUE 131 1 setosa 5.006 3.428
#> 3 0.2645751 FALSE 2 <NA> NA NA
#> 4 0.0000000 TRUE 103 1 setosa 5.006 3.428
#> 5 0.0000000 TRUE 126 1 setosa 5.006 3.428
#> 6 0.0000000 TRUE 130 1 setosa 5.006 3.428
#> # ... with 293 more rows, and 2 more variables: Petal.Length <dbl>,
#> # Petal.Width <dbl>
#> #
#> # Edge Data: 298 x 3
#> from to to_setose
#> <int> <int> <lgl>
#> 1 3 1 TRUE
#> 2 3 2 TRUE
#> 3 7 5 TRUE
#> # ... with 295 more rowsExpanding the vocabulary
On top of what has been showed so far, tidygraph provides an assortment of graph specific verbs that can be used to power your analysis and manipulation. Analogous to bind_rows(), tidygraph provides three functions to expand your data: bind_nodes() and bind_edges() append nodes and edges to the graph respectively. As with the join functions bind_edges() must contain valid from and to columns. bind_graphs() allows you to combine multiple graphs in the same graph structure resulting in each original graph to become a component in the returned graph.
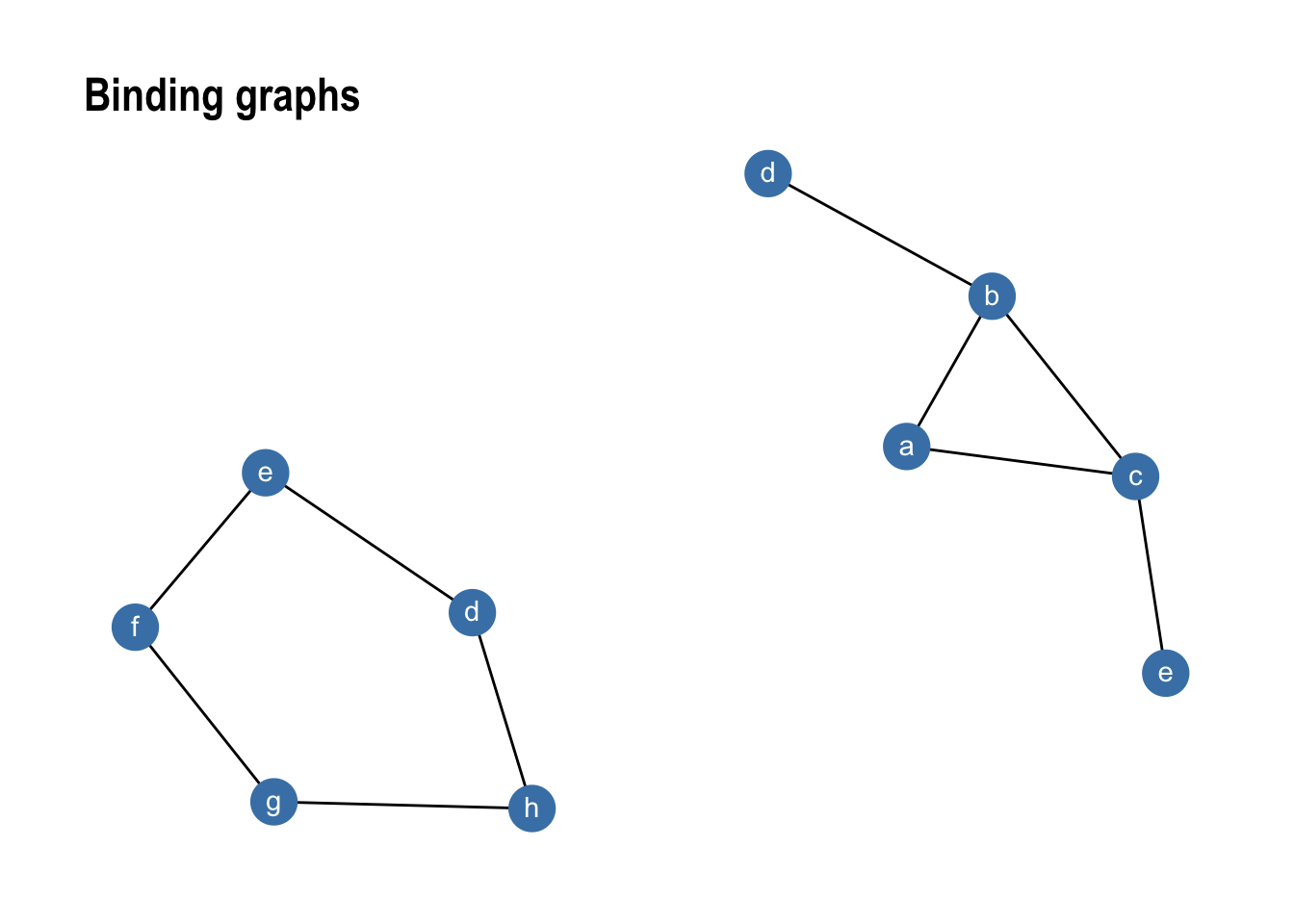
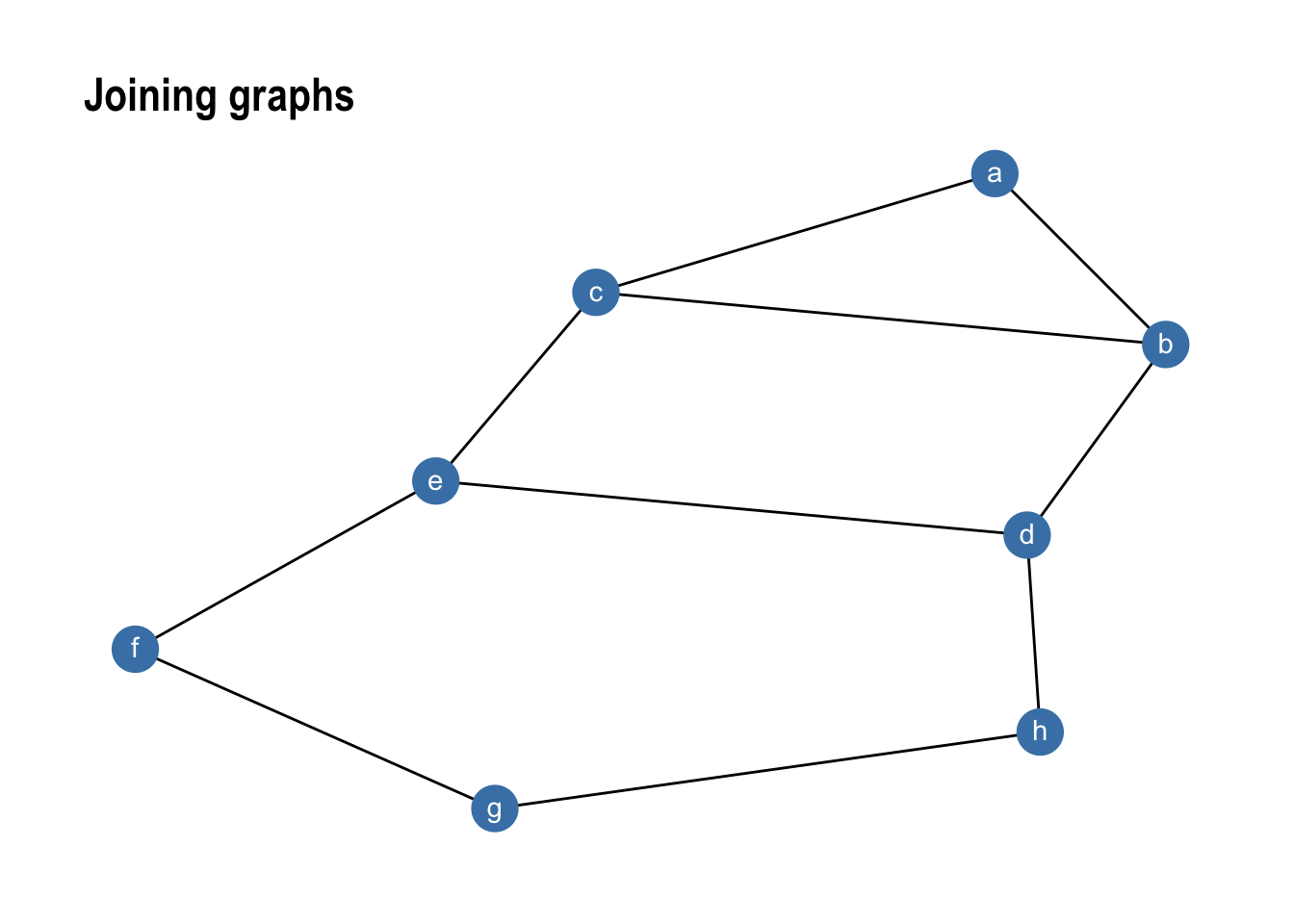
While bind_graphs() cannot be used to create edges between the merged graphs graph_join() can do just that. It merges nodes using a full_join() semantic and keeps the individual edges from both graphs:
library(ggraph)
gr1 <- create_notable('bull') %>%
mutate(name = letters[1:5])
gr2 <- create_ring(5) %>%
mutate(name = letters[4:8])
# Plot
gr1 %>% bind_graphs(gr2) %>%
ggraph(layout = 'kk') +
geom_edge_link() +
geom_node_point(size = 8, colour = 'steelblue') +
geom_node_text(aes(label = name), colour = 'white', vjust = 0.4) +
ggtitle('Binding graphs') +
theme_graph()
gr1 %>% graph_join(gr2) %>%
ggraph(layout = 'kk') +
geom_edge_link() +
geom_node_point(size = 8, colour = 'steelblue') +
geom_node_text(aes(label = name), colour = 'white', vjust = 0.4) +
ggtitle('Joining graphs') +
theme_graph()
The standard dplyr verbs protects the to and from columns in the edge data in order to avoid accidental modification of the graph topology. If changing of the terminal nodes are necessary the reroute() verb will come in handy:
gr1 <- create_star(6, directed = TRUE)
layout <- create_layout(gr1, layout = 'fr')
gr1 <- gr1 %>%
mutate(x = layout$x, y = layout$y, graph = 'original')
gr2 <- gr1 %>%
mutate(graph = 'reverse') %>%
activate(edges) %>%
reroute(from = to, to = from)
gr3 <- gr1 %>%
mutate(graph = 'using subset') %>%
activate(edges) %>%
reroute(from = to + 1, subset = to < 4)
ggraph(bind_graphs(gr1, gr2, gr3), layout = 'nicely') +
geom_edge_link(arrow = arrow()) +
facet_nodes(~graph) +
theme_graph(foreground = 'steelblue')
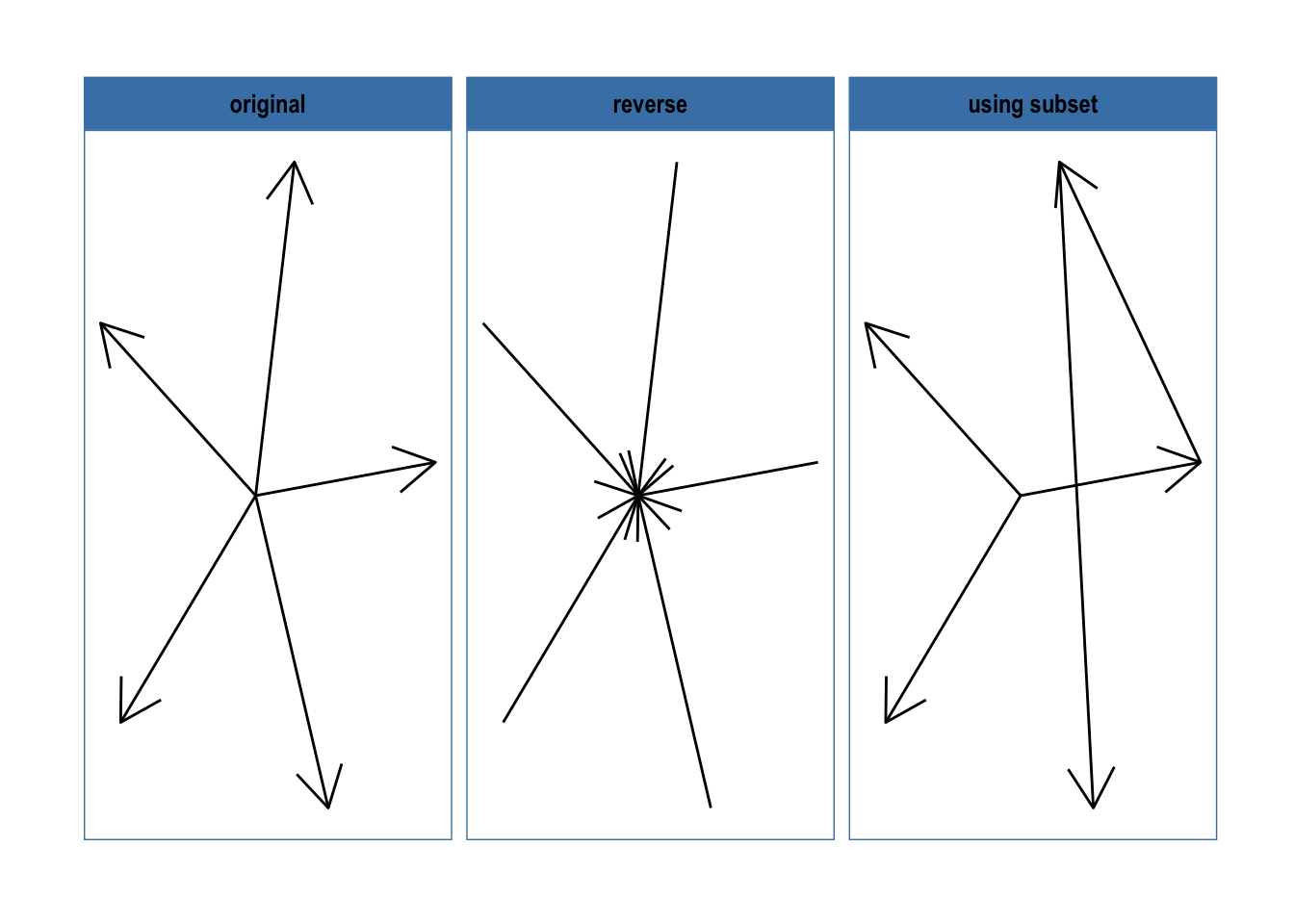
As can be seen, reroute works pretty much as a to and from specific mutate(), with the added benefit of incorporating a subset operator if only a few edges should be changed.
Making the most of graphs
While being able to use the dplyr verbs on relational data is nice and all, one of the reasons we are dealing with graph data in the first place is because we need some graph-based algorithms for solving our problem at hand. If we need to break out of the tidy workflow every time this was needed we wouldn’t have gained much. Because of this tidygraph has wrapped more or less all of igraphs algorithms in different ways, ensuring a consistent syntax as well as output that fits into the tidy workflow. In the following we’re going to take a look at these.
Central to all of these functions is that they know about which graph is being computed on (in the same way that n() knows about which tibble is currently in scope). Furthermore they always return results matching the node or edge position so they can be used directly in mutate() calls.
Node and edge types
On the top of our list of things we might be interested to know about is whether nodes or edges are of specific types such as leaf, sink, loop, etc. All of these functions return a logical vector indicating if the node or edge belong to the specified group. To easily find functions that queries types, all functions are prefixed with node_is_/edge_is_.
create_tree(20, 3) %>%
mutate(leaf = node_is_leaf(), root = node_is_root()) %>%
ggraph(layout = 'tree') +
geom_edge_diagonal() +
geom_node_point(aes(filter = leaf), colour = 'forestgreen', size = 10) +
geom_node_point(aes(filter = root), colour = 'firebrick', size = 10) +
theme_graph()
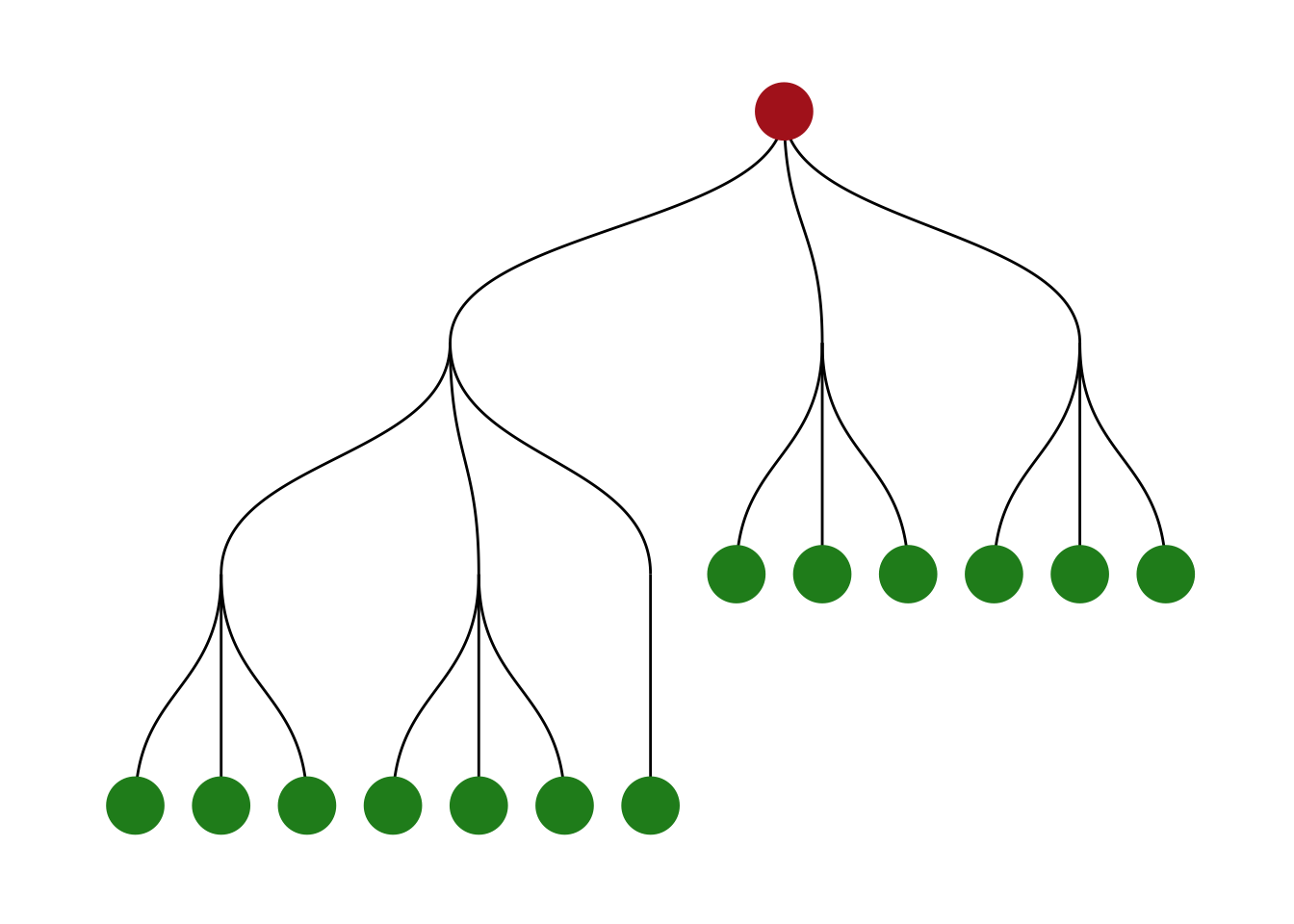
Another example could be to remove loop edges using filter(!edge_is_loop()).
Centrality
One of the simplest concepts when computing graph based values is that of centrality, i.e. how central is a node or edge in the graph. As this definition is inherently vague, a lot of different centrality scores exists that all treat the concept of central a bit different. One of the famous ones is the pagerank algorithm that was powering Google Search in the beginning. tidygraph currently has 11 different centrality measures and all of these are prefixed with centrality_* for easy discoverability. All of them returns a numeric vector matching the nodes (or edges in the case of centrality_edge_betweenness()).
play_smallworld(1, 100, 3, 0.05) %>%
mutate(centrality = centrality_authority()) %>%
ggraph(layout = 'kk') +
geom_edge_link() +
geom_node_point(aes(size = centrality, colour = centrality)) +
scale_color_continuous(guide = 'legend') +
theme_graph()
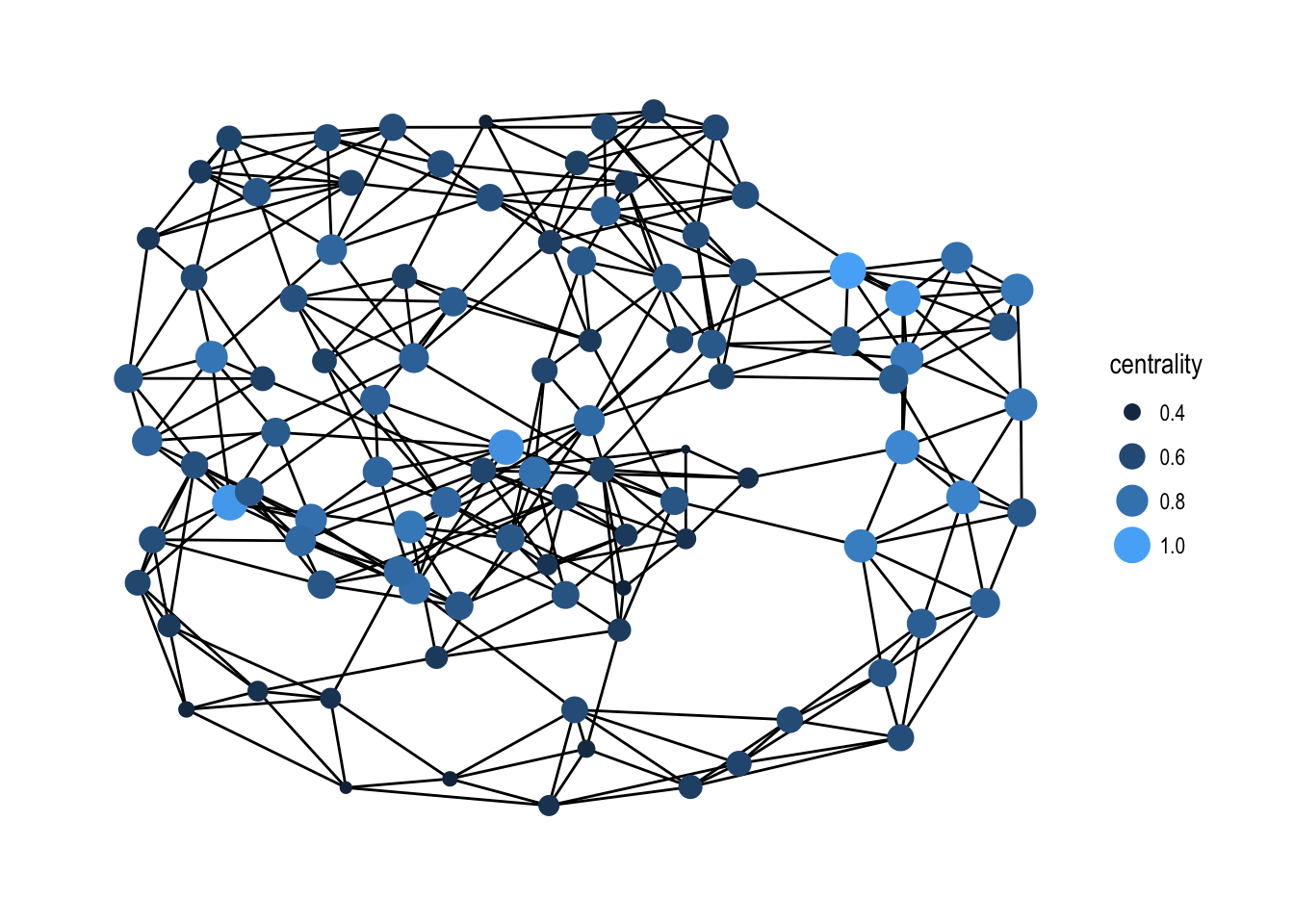
It is quite difficult to a priori decide which centrality measure makes most sense for a problem at hand so having easy access to a large range of them in a common syntax is a boon.
Clustering
Another common operation is to group nodes based on the graph topology, sometimes referred to as community detection based on its commonality in social network analysis. All clustering algorithms from igraph is available in tidygraph using the group_* prefix. All of these functions return an integer vector with nodes (or edges) sharing the same integer being grouped together.
play_islands(5, 10, 0.8, 3) %>%
mutate(community = as.factor(group_infomap())) %>%
ggraph(layout = 'kk') +
geom_edge_link(aes(alpha = ..index..), show.legend = FALSE) +
geom_node_point(aes(colour = community), size = 7) +
theme_graph()
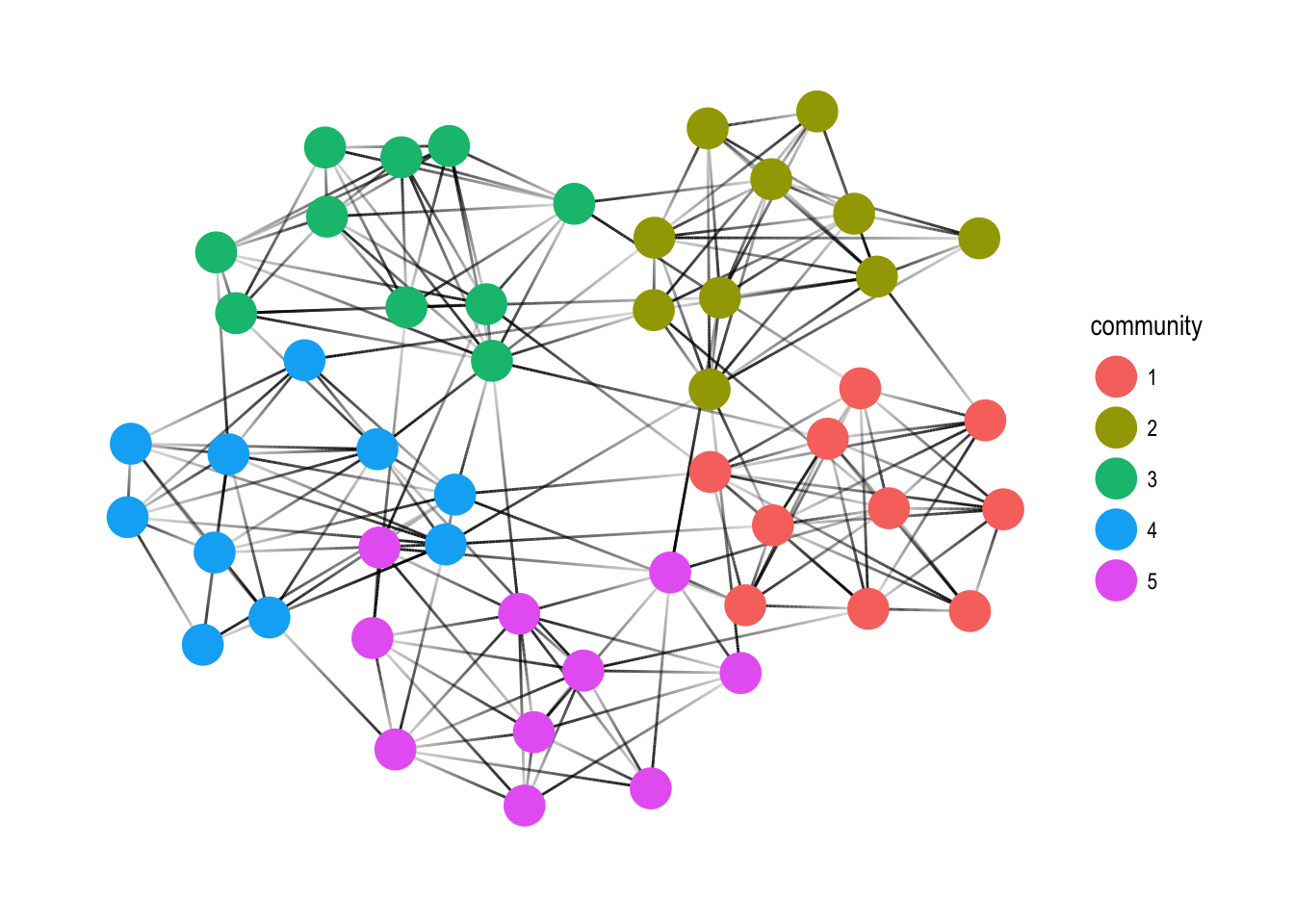
Node pairs
Some statistics are a measure between two nodes, such as distance or similarity between nodes. In a tidy context one of the ends must always be the node defined by the row, while the other can be any other node. All of the node pair functions are prefixed with node_* and ends with _from/_to if the measure is not symmetric and _with if it is; e.g. there’s both a node_max_flow_to() and node_max_flow_from() function while only a single node_cocitation_with() function. The other part of the node pair can be specified as an integer vector that will get recycled if needed, or a logical vector which will get recycled and converted to indexes with which(). This means that output from node type functions can be used directly in the calls, e.g.
play_geometry(50, 0.25) %>%
mutate(dist_to_center = node_distance_to(node_is_center())) %>%
ggraph(layout = 'kk') +
geom_edge_link() +
geom_node_point(aes(size = dist_to_center), colour = 'steelblue') +
scale_size_continuous(range = c(6, 1)) +
theme_graph()
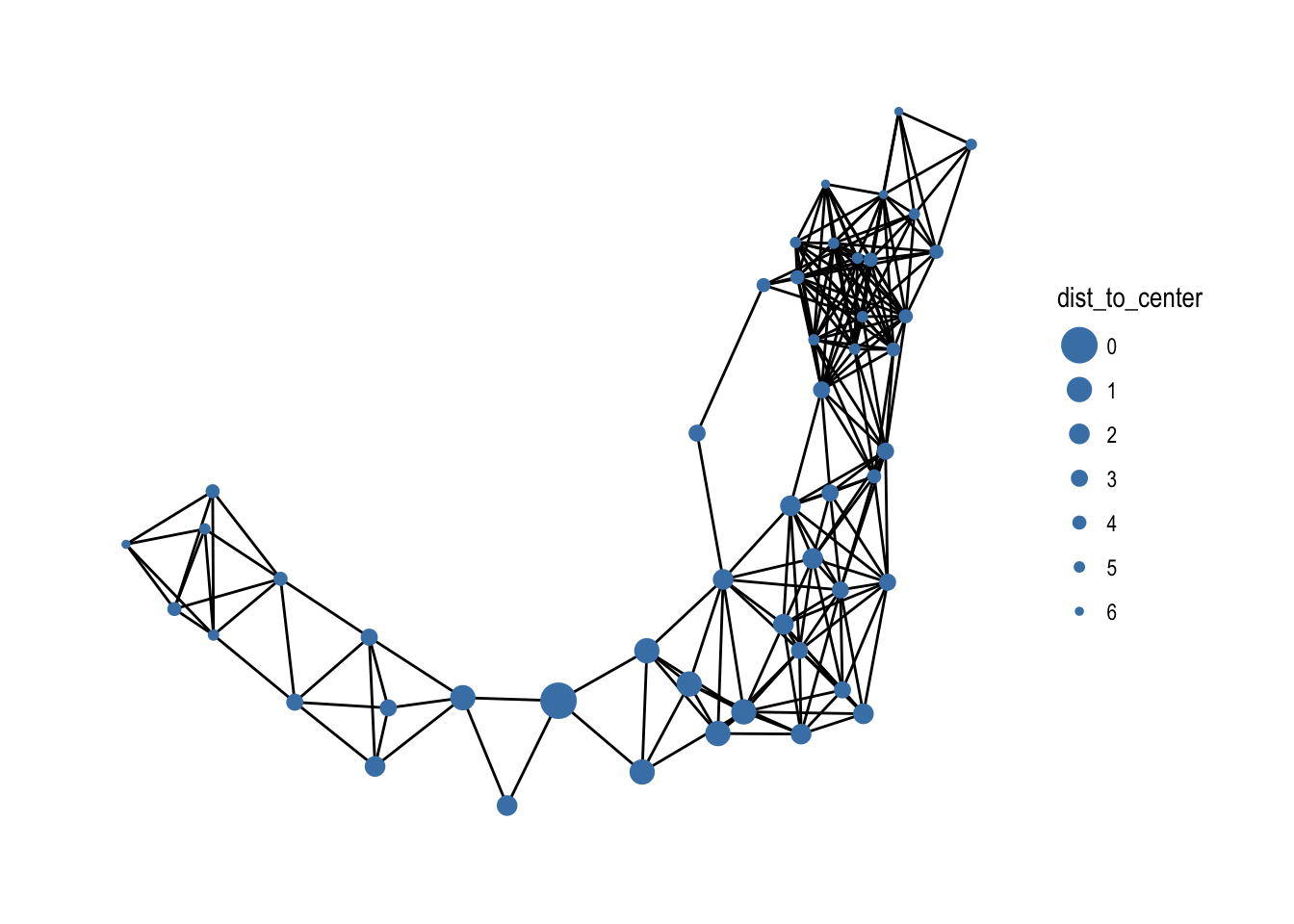
Searches
An integral type of operation on graphs is to perform a search, that is, start from one node and then traverse the edges until all nodes has been visited. The most common approaches are either breath first search where all neighbors of a node is visited before moving on to the next node, or depth first serch where you move along to the next node immediately and only backtracks and visit other neighbors when you’ve hit a dead end. Different statistics from these searches are available in tidygraph through the bfs_() and dfs_() family of functions e.g. the distance to the start node along the search can be obtained with bfs_dist()/dfs_dist(). The root node can be specified in the same way as with node pairs. Sorting based on a search from the node with highest centrality can thus be done with:
play_geometry(50, 0.25) %>%
mutate(order = bfs_rank(which.max(centrality_alpha())))
#> # A tbl_graph: 50 nodes and 227 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 50 x 3 (active)
#> x y order
#> <dbl> <dbl> <int>
#> 1 0.01637861 0.11280499 49
#> 2 0.01721270 0.19181732 50
#> 3 0.02015524 0.74802650 46
#> 4 0.04361792 0.09377818 48
#> 5 0.04622344 0.95686281 47
#> 6 0.07677761 0.46011354 41
#> # ... with 44 more rows
#> #
#> # Edge Data: 227 x 2
#> from to
#> <int> <int>
#> 1 1 2
#> 2 1 4
#> 3 2 4
#> # ... with 224 more rowsLocal measures
Often we find ourselves interested in the local neighborhood of a node for various reasons. We might want to know the average degree around a node or the number of triangles each node participate in. The local_*() family of functions provide access to a range of node measures that are dependent on the local neighborhood of each node.
# Weight the node degree by the average degree of its neighboors
play_smallworld(1, 100, 3, 0.05) %>%
mutate(weighted_degree = centrality_degree() / local_ave_degree())
#> # A tbl_graph: 100 nodes and 300 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 100 x 1 (active)
#> weighted_degree
#> <dbl>
#> 1 0.8064516
#> 2 1.0000000
#> 3 0.8064516
#> 4 1.2075472
#> 5 0.9729730
#> 6 0.6153846
#> # ... with 94 more rows
#> #
#> # Edge Data: 300 x 2
#> from to
#> <int> <int>
#> 1 1 2
#> 2 2 3
#> 3 4 97
#> # ... with 297 more rowsAll the rest
While an ontology of graph operations has been attempted in the different functions above, there are some that falls outside. These have been lumped together under the node_() and edge_() umbrellas and include things such as topological ordering and Burt’s constraint among others. All of these functions ensures a mutate-compatible output.
Graph measures
Along with computations on the individual nodes and edges it is sometimes necessary to get summary statistics on the graph itself. These can be simple measures such as the number of nodes and edges as well as more involved measures such as assortativity (the propensity of similar nodes to be connected). All of these measures can be calculated through the graph_*() function family and they will all return a scalar.
# Normalise the node pair adhesion with the minimal adhesion of the graph
play_islands(5, 10, 0.7, 3) %>%
mutate(norm_adhesion = node_adhesion_to(c(50, 1:49)) / graph_adhesion())
#> # A tbl_graph: 50 nodes and 181 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 50 x 1 (active)
#> norm_adhesion
#> <dbl>
#> 1 1.75
#> 2 2.00
#> 3 2.25
#> 4 1.75
#> 5 1.50
#> 6 1.50
#> # ... with 44 more rows
#> #
#> # Edge Data: 181 x 2
#> from to
#> <int> <int>
#> 1 1 2
#> 2 1 3
#> 3 2 3
#> # ... with 178 more rowsMapping over nodes
Just to spice it all up a bit tidygraph pulls purrr into the mix and provides some additional graph-centric takes on the familiar map*(). More specifically tidygraph provides functionality to apply a function over nodes as a breath or depth first search is carried out, while getting access to the result of the computations coming before, as well as mapping over the local neighborhood of each node. All of these function returns a list in their bare bone form, but as with purrr versions exists that ensures the output is of a certain type (e.g. map_bfs_dbl()).
Mapping over searches
The search maps comes in two flavors. Either the nodes are mapped in the order of the search, or they are mapped in the reverse order. In the first version, each call will have access to the statistics and map results of all the nodes that lies between itself and the root. In the second version each call will have access to the results and statistics of all its offspring. Furthermore the mapping function is passed the graph itself as well as all the search statistics of the node currently being mapped over. An example would be to propagate the species value in our iris clustering upwards as long as theirs agreement between the children. For this to work, we will need the reverse version of a breath first search to make sure that all children have been evaluated prior to mapping over a node:
iris_tree <- iris_tree %>%
activate(nodes) %>%
mutate(Species = map_bfs_back_chr(node_is_root(), .f = function(node, path, ...) {
nodes <- .N()
if (nodes$leaf[node]) return(nodes$Species[node])
if (anyNA(unlist(path$result))) return(NA_character_)
path$result[[1]]
}))
ggraph(iris_tree, layout = 'dendrogram') +
geom_edge_diagonal2(aes(colour = node.Species)) +
theme_graph()
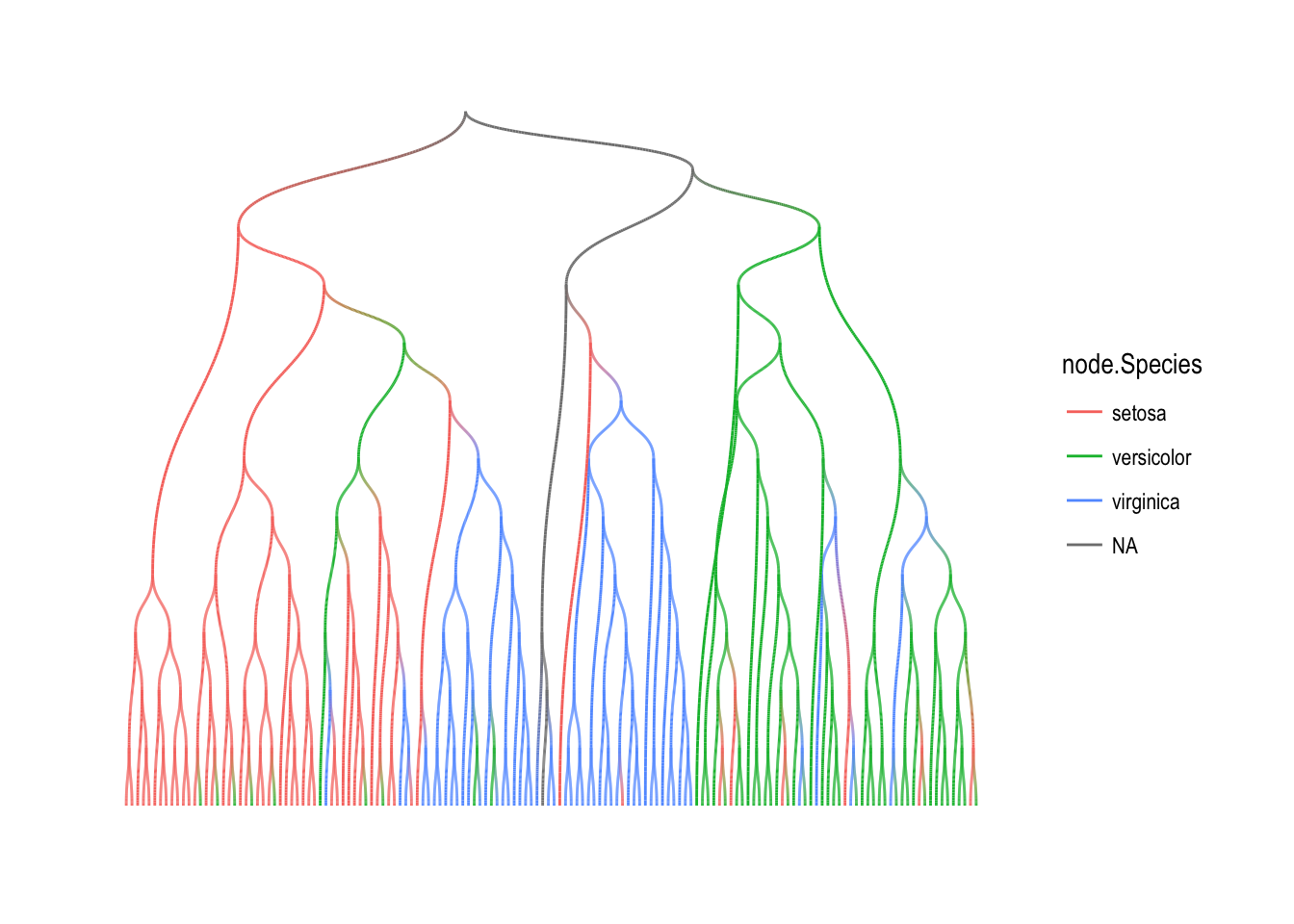
Mapping over neighborhoods
The neighborhood map is exposed through map_local() as well as its type safe versions. The mapping function has a much simpler format as it simply gets passed a subgraph representing the local neighborhood as well as the index of the node in the original graph being mapped over. E.g. to get the number of edges in the local neighborhood around each node, one would simply do:
play_smallworld(1, 100, 3, 0.05) %>%
mutate(neighborhood_edges = map_local_dbl(.f = function(neighborhood, ...) {
igraph::gsize(neighborhood)
}))
#> # A tbl_graph: 100 nodes and 300 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 100 x 1 (active)
#> neighborhood_edges
#> <dbl>
#> 1 14
#> 2 14
#> 3 13
#> 4 15
#> 5 12
#> 6 14
#> # ... with 94 more rows
#> #
#> # Edge Data: 300 x 2
#> from to
#> <int> <int>
#> 1 1 2
#> 2 2 3
#> 3 3 4
#> # ... with 297 more rowsOne last thing…
While the functions discussed above makes it easy to make slight changes to your network topology it is less straightforward to make radical changes. Even more so if the radical changes are only needed temporarily for the sake of a few computations. This is where the new morph() verb comes in handy (along with the accompanying unmorph() and crystallise() verbs). In essence, morph() lets you set up a temporary alternative version of your graph, make computations on it using the standard dplyr verbs, and then merge the changes back in using unmorph(). The types of alternative representations are varied and can be extended by the user. Nodes can be converted to edges and the other way around, both nodes and edges can be combined, and the alternate representation does not need to cover the full original graph. Instead of trying to describe it in words, let’s see how it plays out in use:
islands <- play_islands(5, 10, 0.8, 3) %>%
mutate(group = group_infomap())
# Get the distance to the central node in each group
islands <- islands %>%
morph(to_split, group) %>%
mutate(dist_to_center = node_distance_to(node_is_center())) %>%
unmorph()
islands
#> # A tbl_graph: 50 nodes and 211 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 50 x 2 (active)
#> group dist_to_center
#> <int> <dbl>
#> 1 5 0
#> 2 5 0
#> 3 5 0
#> 4 5 0
#> 5 5 0
#> 6 5 0
#> # ... with 44 more rows
#> #
#> # Edge Data: 211 x 2
#> from to
#> <int> <int>
#> 1 1 3
#> 2 2 3
#> 3 1 4
#> # ... with 208 more rows
# Get the number of edges exiting each group
islands <- islands %>%
morph(to_contracted, group, simplify = FALSE) %>%
activate(edges) %>%
filter(!edge_is_loop()) %>%
activate(nodes) %>%
mutate(exiting_group = centrality_degree(mode = 'out')) %>%
unmorph()
islands
#> # A tbl_graph: 50 nodes and 211 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 50 x 3 (active)
#> group dist_to_center exiting_group
#> <int> <dbl> <dbl>
#> 1 5 0 12
#> 2 5 0 12
#> 3 5 0 12
#> 4 5 0 12
#> 5 5 0 12
#> 6 5 0 12
#> # ... with 44 more rows
#> #
#> # Edge Data: 211 x 2
#> from to
#> <int> <int>
#> 1 1 3
#> 2 2 3
#> 3 1 4
#> # ... with 208 more rows
# Calculate an edge centrality score by converting to the linegraph
islands <- islands %>%
morph(to_linegraph) %>%
activate(nodes) %>%
mutate(edge_centrality = centrality_pagerank()) %>%
unmorph()
islands
#> # A tbl_graph: 50 nodes and 211 edges
#> #
#> # An undirected simple graph with 1 component
#> #
#> # Node Data: 50 x 3 (active)
#> group dist_to_center exiting_group
#> <int> <dbl> <dbl>
#> 1 5 0 12
#> 2 5 0 12
#> 3 5 0 12
#> 4 5 0 12
#> 5 5 0 12
#> 6 5 0 12
#> # ... with 44 more rows
#> #
#> # Edge Data: 211 x 3
#> from to edge_centrality
#> <int> <int> <dbl>
#> 1 1 3 0.005117026
#> 2 2 3 0.005079217
#> 3 1 4 0.004657749
#> # ... with 208 more rows
As can be seen, the morph syntax both handles multiple graphs, collapsed nodes and changing edges to nodes, without any change in the mental model of the operations. All morphing functions are prefixed with to_* for easy discovery and includes minimum spanning trees, complement graph, dominator tree etc. In the case where you are interested to continue working with the morphed representation as a proper tbl_graph you can use the cystallise() verbs that removes any link to the original graph and returns a tibble with a row per graph in the morphed representation (as a morph can result in multiple graphs):
islands %>%
morph(to_split, group) %>%
crystallise()
#> # A tibble: 5 x 2
#> name graph
#> <chr> <list>
#> 1 group: 1 <S3: tbl_graph>
#> 2 group: 2 <S3: tbl_graph>
#> 3 group: 3 <S3: tbl_graph>
#> 4 group: 4 <S3: tbl_graph>
#> 5 group: 5 <S3: tbl_graph>Wrapping it all up
I hope I have given you a small glimpse of what tidygraph is all about. If working with network data in the past has felt intimidating and strange tidygraph might feel more at home, but even if you’re a seasoned pro within network analysis the package should provide a powerful but streamlined interface to many operations.
Roadmap
The next goal of my quest to revamp relational data analysis in R will be to “rebuild” ggraph around tidygraph. This is not to say that the two are incompatible at the moment — there’s full support through ggraphs support for igraph — rather I want to only support tbl_graph in the future as all relevant data structures can be converted to this common format through as_tbl_graph().
For tidygraph itself, I have some more ideas I want to explore. Currently missing from the whole package is any notion of modelling and it will be interesting to see how this can fit in. Further, I have this wild idea about providing a tidygraph link to graph databases such as Neo4J in the same way as dbplyr provides an interface to SQL databases. Lastly, the current focus has been on supporting the algorithms provided by igraph. While an extensive package, igraph does not implement everything and there might be stuff lacking that should be added down the line.
Take care…